Je me suis amusé à faire une feuille de calcul toute simple dans un tableur : je pars d'une valeur initiale (100 ou 1000), et sur chaque ligne je rajoute 2% de la valeur précédente. Le fichier Open-Office correspondant est disponible ici.
Je réitère l'opération quelques centaines de fois, et j'obtiens les courbes suivantes :
C'est une évidence, mais ça ne fait pas de mal de le voir sur une courbe : un taux de croissance, même faible (2%), entraîne une croissance exponentielle.
C'est une croissance infinie : peu importe la valeur initiale, au bout d'un temps suffisant, on peut dépasser n'importe quelle valeur choisie arbitrairement.
Ce n'est pas lié à un facteur d'échelle particulier : si on zoom sur la partie de la courbe rouge qui semble plate (entre 0 et 200), on obtient :
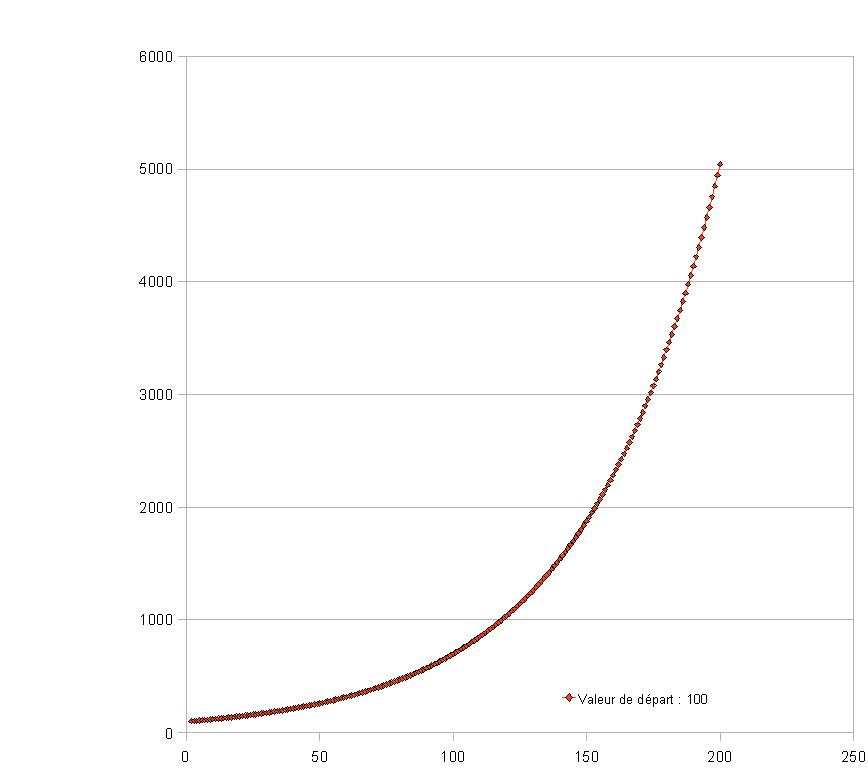
(cliquer sur l'image pour agrandir)
A tous nos amis journalistes, économistes et politiques, qui guettent fébrilement les signes du retour de la sainte croissance, comme jadis les paysans attendaient impatiemment la pluie ; un beau jour il faudra quand même poser la question : la croissance, jusqu'où ?
Quand Nicolas Sarkozy déclare "la croissance, j'irai la chercher" (voir article), j'ai bien envie de lui répondre : cherche bien partout, et surtout quand tu l'auras trouvée, restes-y !! :)
Et pour conclure, terminons par une citation de l'économiste Kenneth Ewart Boulding :
Toute personne croyant qu'une croissance exponentielle peut durer indéfiniment dans un monde fini est soit un fou, soit un économiste.






7 commentaires:
C'est pas ça qu'on appelle "la fuite en avant", dans le jargon ? =)
Bon, tu mériterais presque un "et alors ?", mais j'ai peur que tu le prennes mal...
Donc, tu as démontré qu'une donnée croissant de manière exponentielle sur une longue durée tendait vers l'infini. Bien. Tu as effectivement des lecteurs que ça pourrait intéresser, cette découverte fondamentale (par exemple, ma fille de 5 ans, qui avait déjà bien aimé les bufles, et, qui me demandait hier soir : "c'est quoi la Science ?", en réponse à une question de son frère, 3 ans, qui me demandait "C'est quoi la fête de la Science ?". Il va de soi que je n'ai pas répondu).
Hé hé, j'aime bien les longues parenthèses.
Bref, tu as fais le plus simple. Ce n'aurait pas été le cas par exemple si tu avais voulu expliquer que la somme infinie d'éléments finis n'est pas forcément infinie.
Ou aborder ce concept intéressant qui plutôt que de parler "d'exponentielle" parle "d'entropique".
Bon, ne tournons pas autour du pot : ce qui pose problème dans la notion de croissance, telle qu'elle est définie aujourd'hui en économie, c'est qu'elle se limite à la croissance DU PIB, ET SEULEMENT DU PIB. Or, tout un tas d'éléments tels que la "qualité de vie" ne sont pas pris en compte. C'est donc plus dans la critique de la DEFINITION de la croissance, plus que dans celle de la notion de croissance elle-même que se trouve actuellement selon moi les contributions les plus "riches", de la part notamment des tenants de l'a-croissance.
En corollaire, cela conduit à limiter en particulier le coût écologique de la croissance. Par exemple, on peut pense qu'un service vendu à distance et au même prix qu'une intervention "à domicile" génère la même croissance économique que cette dernière, sans avoir le même coût en ressources.
Ou encore, pour faire un parallèle, quand tu recherches une progression professionnelle (on pourrait dire croissance professionnelle), tu ne vas pas regarder que ton salaire, mais aussi la qualité du relationnel avec les équipes (qui lui ne "coûte" pas grand-chose en tant que tel...).
C'est ainsi que l'éducation par exemple est une richesse qui ne se mesure pas aujourd'hui dans la croissance, en tout cas de manière directe. Un pays qui compte de moins en moins d'illetrés n'est pas considéré en croissance, alors qu'il l'est objectivement autant qu'un pays ou le nombre de console WII augmente (c'est un exemple, hein).
Ainsi, il ne me semble pas illusoire de penser que la croissance peut-être infinie, si la consommation des ressources sur lesquelles elle se base n'est elle pas infinie.
Merci de me permettre grâce à ton billet de m'exprimer sur ce sujet à la mode, mais passionnant.
J'ai toujours été une bille en maths. Donc c'est parfait, ta fille me filera des cours.
Le fait que le contexte économique morose qui est le notre corresponde en fait à une croissance exponentielle du PIB, je trouve ça assez marrant.
Ce qui est moins marrant, c'est qu'à mon avis à court terme cette croissance va prendre un sacré coup de plomb dans l'aile, en particulier à cause de notre dépendance en pétrole. J'y reviendrai, c'est l'objet de mon prochain billet.
Sinon, je pense qu'on est bien d'accord : on nous bassine sans arrêt avec cette histoire de croissance du PIB. C'est le but de ce message : insister sur le non-sens qu'il y a à mettre la croissance du PIB au coeur de la doctrine économique. Surtout lorsque le modèle social est refaçonné selon cette doctrine. Voir par exemple le rapport de la "Commission pour la libération de la croissance française" dirigée par Jacques Attali : http://agoravox.fr/article.php3?id_article=30304
J'ai vu passer quelques articles intéressants à propos du PIB sur AgoraVox, par exemple : http://agoravox.fr/article.php3?id_article=30690 et http://www.agoravox.fr/article.php3?id_article=20303
Cet article ( ftp://ungaro.u-bourgogne.fr/asrdlf/papiers/Maillat.pdf ) présente un certain nombre "d'indicateurs de bien-être".
J'ai en mémoire une interview de Jean-Pierre Berlan (ex-Directeur de recherche à l'INRA). Pour un problème particulier de lutte contre un parasite, il montre de quelle manière l'amélioration du bien-être a pu se faire parallèlement à une diminution du PIB (à moindre coût, sans avoir recours à ni à des engrais chimiques ni a des pesticides, à la fois couteux et polluants). J'essairai de remettre la main là-dessus.
En matière d'écologie en particulier, je pense qu'on ne pourra pas prendre le problème par le bon bout tant que la "croissance" (du PIB) sera considérée comme quelque chose de sacré. Pour ça, il faut des hommes politiques pas trop débiles, et qui aient un minimum de courage (voir : http://lelab.tv/video/11460d394bdc5b9 ). Que Goasguen soit aussi lamentable et aussi ridicule, ça peut prêter à sourir. Mais je crois que cette interview est assez symptomatique de l'aveuglement des illuminés de la croissance.
En fait, tu as raison, on est d'accord.
J'aurais du le préciser : je n'écris pas des commentaires QUE pour être contradictoire... ;-)
Ah ça se passe ici maintenant, alors je bisse :
Oui, le problème aussi vient de l'indicateur utilisé pour calculer la croissance. C'est le PIB. Or le PIB ne fait aucune différence entre les activités socialement utiles et celles globalement nuisibles (comme les compétitions automobiles par exemple !)
En divisant 70 par le taux de croissance, on obtient approximativement le temps de doublement. Si le taux n'est pas trop grand.
soit 35 ans pour 2%.
Quand à la phrase :
"Toute personne croyant qu'une croissance exponentielle peut durer indéfiniment dans un monde fini est soit un fou, soit un économiste."
Pour ma part, aimant tendre vers l'exhaustif, je dirais plutôt :
"Toute personne croyant qu'une croissance exponentielle peut durer indéfiniment dans un monde fini peut être un fou ou un économiste. Car l'un n'empêche pas l'autre."
belle journée à vous, Didier
It is fascinating to see how a small percentage increase can lead to exponential growth over time.
Enregistrer un commentaire